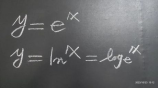掌握旋转矩阵，从线性代数入手

旋转矩阵是线性代数的基本概念之一，通俗的讲，它是用于描述一个向量在二维或三维空间中旋转的矩阵。掌握旋转矩阵不仅有助于我们更好地理解线性代数的基本概念，也能广泛应用于计算机图形学、机器人学等方面。

旋转矩阵的计算方法有多种，其中最常用的是欧拉公式。利用欧拉公式的定义推导可得，欧拉矩阵可以表示三个不同轴向的旋转。根据欧拉角定义的不同，欧拉矩阵有多种变形，例如与口诀z-y'-x'有关的ZYX欧拉矩阵。

在计算机图形学中，旋转矩阵常被用于描述物体在三维空间中的变形。例如，我们可以通过不同的旋转矩阵将一个三维模型呈现出不同的角度。此外，在机器人学中，旋转矩阵也起着至关重要的作用。机器人的运动包括平移和旋转，其中旋转就需要利用旋转矩阵来描述转动的方向及幅度。